[건축-지어지지 않은 20세기] 04 움직이는 기하학_봉일범

건축가들이 사용하는 기하학은 공간과 이용자의 행동에 영향을 준다.

 

# 칸= 피터 아이젠만+안도 다다오

 

 

마인드맵 1

루이스 칸은 정사각형 원형 등 기하학을 주로 사용하는 건축가로 기억하고 있다. 그 기하학이라는 것에도 정도와 방향이 다양하다. 루이스 칸은 피터아이젠만이 가지고 있었던 기하학의 구성원리를 객관적으로 설정하려는 경향을 가지고 있었다(정사각형 내에서 order를 만들려고 하는). 하지만 피터 아이젠만 처럼 완전히 그것을 공간을 만드는 구성원리로 사용하지는 않았다. 오히려 건축을, 즉물적인 무언가를 만들어내려고 할 때는 안도 다다오처럼 기하학을 직관과 경험의 도구로서 사용하였다.

 

왼) 피터 아이젠만 우) 안도 다다오

 

# 기하학의 종류(type of geometry) / 건축가들이 쓰는 기하학

 

피타고라스의 정리. 고전 기하학

위상(위계)적으로 저것들은 동일하다, 위상 기하학

평면이 아닌 구 휜평면 위에서의 기하학은 달라진다. 비 유클리드 기하학

 

우리가 평소에 알고 있는 피타고라스의 정리나 삼각형의 내합의 합은 180도. 등의 정의는 모두 유클리드 기하학에서 비롯 되었다. 하지만 비 유클리드 기하학, 프랙탈 기하학, 위상 기하학등 다양한 기하학이 현대에는 존재한다. 하지만 건축은 건축주 또는 일반인들에게 공감을 얻어야만 살아남을 수 있는 성질을 가지고 있기에 아직도 고전기하학을 주로 사용한다. 그리고 그 사용한다는 기하학도 거의 이미지 수준으로 사용한다. 건축가 중에 정오면체 작도법이나, 정사면체를 그리는 방법을 아는 사람이 몇이나 되겠는가. 직감과 경험의 툴로서 사용하는 것이다.

 

 

# 앤팅과 칸 / 예일 대학교 미술관 천장

 

마인드맵 2

 

 

예일 대학교 미술관, 정사면체 모듈로 구성되며 그 위에 플랫슬라브를 올렸다.

앤팅을 만나기 전 칸은 자신만의 참조도구가 없었다(르꼬르뷔제의 필로티와 같은 건축가들의 언어, 디자인프로세스 등등). 앤팅은 기하학을 중심으로 전체를 구축하는 것에 관심이 많은 직원이었다. 그 중 삼각형에 관심을 많이 가졌다. 그러한 2d 삼각형이 발전하여 예일대학교 미술관에서는 정사면체로 발전한다. 정사면체들이 모여있으면 그 삼각형들 사이로 빈공간이 발생한다. 그 공간에 설비 등을 배치한다. 구조-공간이 통합된 'room' 개념으로 발전하는 계기가 되는 작업이라고 할 수 있다. 

 

책을 읽다가 이해가 안되어서 모델링을 해보니 꽤나 상상만으로는 상상하기 힘든 void 모양이 나오니 한번 모델링 해보는 것을 권한다. 그리고 실제 정사면체 거푸집을 시공할 때 어떻게 만들었을지 궁금하다. 시공 짱짱

 

그런 앤팅의 삼각형에는 큰 한계가 있었다. 바로 삼각형의 자기결정성이 매우 크다는 것이다. 즉 삼각형으로의 구축이 거의 답이 나와있는 것이다. 칸은 이것이 굉장히 와닿지 않았다. 하지만 초기에는 이것조차 없었기에 굉장히 긍정적으로 사용하다가 나중에 앤팅과 결별하게 된다.

 

 

# 이원심_숲속의 집- 세지마 카즈요 

 

 

저자가 수록한 모든 작품 중에 가장 진보된 작품의 예로 드는 것이 세지마 카즈요의 숲속의 집이다. 첫 눈에 봐도 굉장히 간명한 기하학으로 만들어진 작품이다. 원이라는 기하학을 사용한 이유는 이 사이트가 울창한 숲으로 둘러 쌓여 있어서 어떤 방향성을 제공하는 주변 컨텍스트가 없었기에 기하학 중 가장 환원적이고 자기 완성적인 원을 사용하였다고 한다. 하지만 왜 원의 중심을 엇갈리게(겹치지 않게) 했는지에 대한 언급은 없다.

중심의 작은원, 전시공간으로 사용된다. 울창한 나무 숲들과 천창이 관련이 있다고 한다.

내부 공간을 주목하라 공간의 볼륨이 달라지고 프로그램은 바뀌고 시각도 한정되지만 공간은 끊어지지 않았다. 이 모든게 원 두개로 만들어졌다.

하지만 엇갈림으로써 공간의 볼륨이 점점 달라진다. 그리고 공간은 굉장히 연속적이지만 이용자의 시각이 한정되기 때문에 연속적이지만 불연속적인 공간을 만들어 낸다(Smooth space)

 

굉장히 단순한 기하학(원 두개)에 간단한 조작(중심을 엇갈림,이원심)을 통하여 매우 풍부하고 다채로운 공간을 만들어 낸 것, 이것이 칸 아이젠만 안도의 근대 건축가들보다 진일보했다라고 부르는 이유이다.

 

 

# 워싱턴 대학, 정육면체 트러스

 

마인드맵 3

 

앤 팅과의 이별이 삼각형/정사면체가 만들어내는 답답한 자기 결정성이었지만 아직 자기만의 체계를 확실히 만들어 내지 못했던지 워싱턴 대학 프로젝트에서 칸은 정육면체 트러스를 이용한다. 정사면체트러스(구조)와의 차이점은 사람이 사용하는 수평면과 가구등 프로그램과의 이질성이 더 적다는 것이다. 그래서 생긴것은 매우 딱딱한 구조지만 개념적으로는 구조의 오더와 공간의 오더를 통합할 수 있는 기하학이었던 것이다.

 

칸은 미스가 잡아놓은 공간 이라는 것이 단지 면적에 불과하다고 말한다. 단위 공간의 본성을 찾아서 그것을 먼저 만족시켜야 한다고 주장한다. 그리고 그 만족이 어떤 물리적인 증거로서 남아야 한다고 말했다. 하지만 그가 해놓은 작업은 대부분이 정사각형이다. 거실도,부엌도,방도 모두 같은 크기의 정사각형인대 어떤 본성을 담았는지 저자는 궁금증을 갖는다. 합리적인 의심이다.

 

 

# 드보어 주택과 팔라디오

마인드맵 4

팔라디오에는 기본적인 기하학을 비율로 쪼개는 행위를 한다. 거기서 칸이 배운것은 공간에 질서를 부여하는 행위. 그것이 가장 잘드러난 것이 드보어 주택이라고 주장한다. 그 질서라는 것이 우리의 상식과는 다른 것으로 보인다. 그에게 그 질서란 방들의 독자성이 살아있는 것, 저 방 abcd가 개별적으로 움직이는 것을 질서라고 불렀다. 그리고 그것은 구조와 공간이 합쳐진 'room'개념과 닿는다. 그것은 근대 건축의 'open plan'과는 다른 개념으로 구별된다.

 

# 내피와 외피 그 중간의 공간 / Hollow Column

마인드 맵 5

 

트렌튼 탈의장

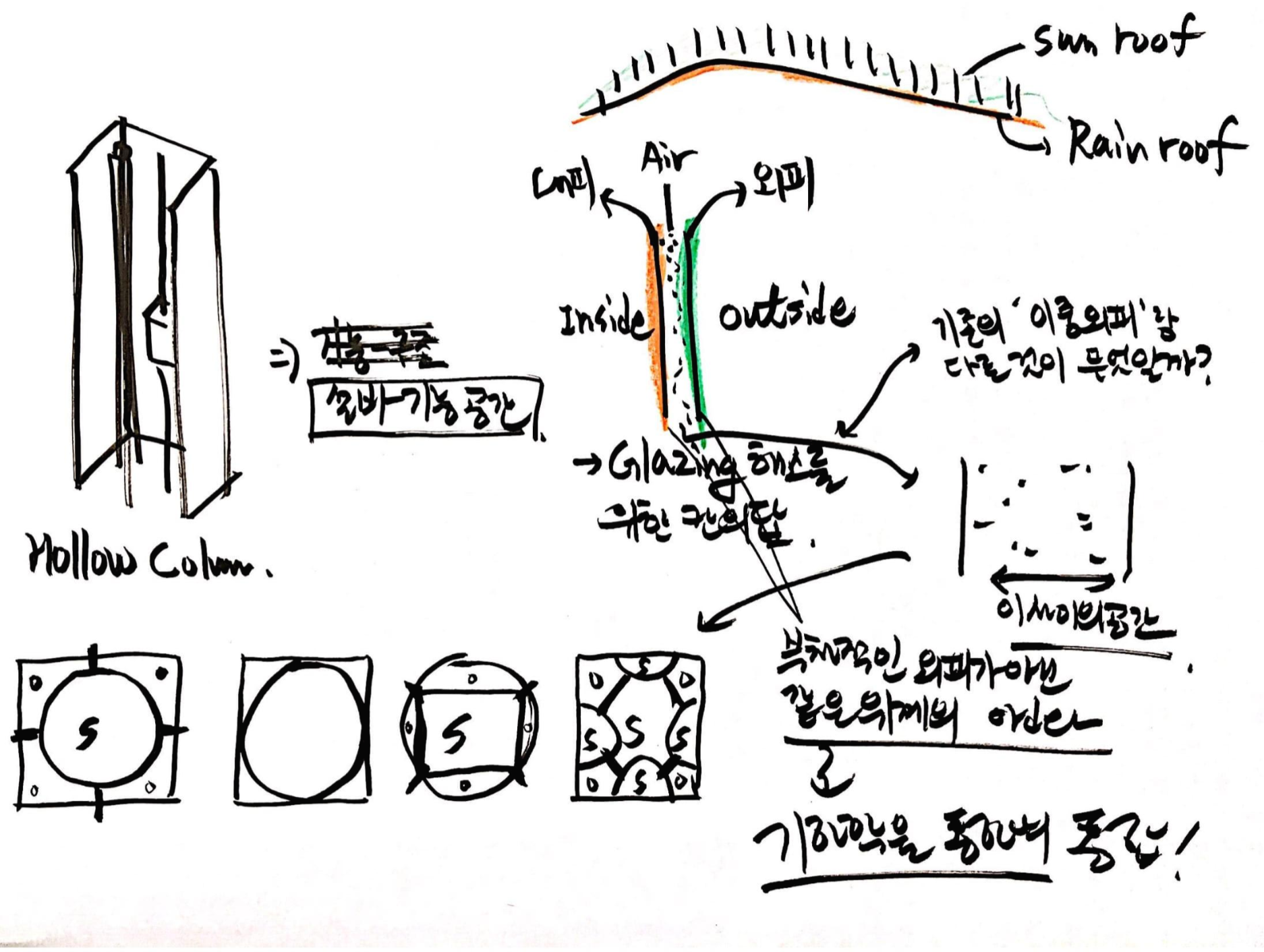
저 정사각형 모퉁이에 ㄷ 형태의 구조가 hollow column이다. 기능-설비공간으로 통합된 구조를 추구했던 루이스칸의 언어이다.

 

제 1유니테리언 교회/ 앙골라 주재 미국 영사관

우리가 흔히 이중외피라고 부를 때 두 외피간의 주부가 존재한다. 부가 되는 외피는 거의 장식용으로 치부당한다. 하지만 루이스 칸은 전체를 하나로 아우르는 것을 추구했던 사람이다. 그래서 인지 내피와 외피의 위계가 동일한 상황을 상상했다. 그래서 외피가 뜨거운 앙골라의 태양을 막아주기는 하지만 통상적인 이중외피처럼 장식적으로 받아지지 않게 하려고 하였고 , 그 방법으로 기하학을 통한 통합을 이용하였다.